A simple Strategy to stop SARS-Cov-2 and fully reopen the Economy
Author: Martin Mindorf
Published: May 5th, 2020
Revision: 1.0
Introduction
This paper is divided into two parts, Part 1 describing the strategy and how to execute it, and Part 2 arguing why it will work. The strategy is designed to be very effective while letting the economy fully reopen.
Part 1
The strategy is designed to be effective in any form of government, but we shall consider it for a democratic society. The role of the government is to lead, inform of the strategy, provide healthcare, testing and funding for sick leave.
The government must clearly communicate the following in writing, by television, newspaper, and students in school must be taught the rules:
– A person who feels sick must immediately isolate and call their doctor to be tested for the virus.
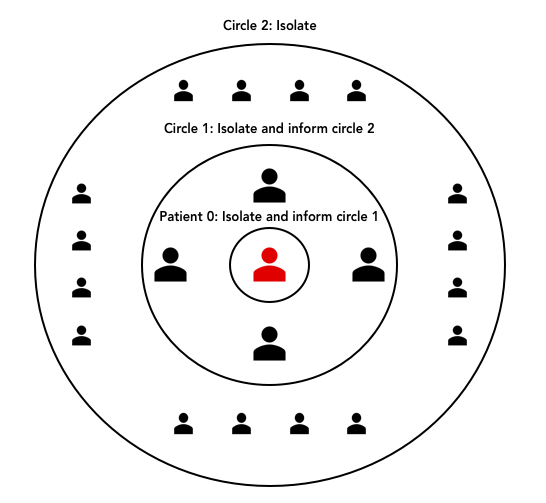
– If a person tests positive for the virus, this person must isolate until they feel well, and for at least 21 days. The person must inform all of their contacts from the last 14 days, including friends, coworkers and anybody who they have been in contact with. These contacts are known as Circle 1.
– All persons in Circle 1 must also isolate for 21 days, and all persons in Circle 1 must contact the persons they have been in contact with for the last 14 days. These contacts are known as Circle 2.
– All contacts in Circle 2 must also isolate for 21 days. Circle 2 doesn’t need to contact anyone.
The person who tested positive, circle 1 and circle 2 should receive full salary during their isolation, and they should work from home. If it is not possible to work from home, their employers should still pay salary, and be compensated for the salary by the government.
Under these circumstances, the economy can almost fully reopen straight away. Restaurants for instance can easily reopen. As long as we know the people that we dine with. Only very large social gatherings like festivals, or tightly packed spaces with a lot of interaction like nightclubs where interaction happen with unknown people, should wait until the number of detected cases reaches and stays at 0 for 1 month. Young people will still be able to meet and socialize at private parties, where there is a known guest list.
The normal societal functions like restaurants, shops and workplaces that open must still display good hygiene.
For the first months, many people will be in circles 1 and circles 2, and not all will be able to go out, but this problem will quickly go away, if people follow the strategy, as the number of new cases will quickly slow.
The strategy will be challenged because many governments have already done a partial reopening, and there will be deaths and a lagged effect from this. Therefore, the strategy should be given 30 days to work from when it is implemented, before the numbers show its effectiveness.
Here is an example in practice: Jens is a school classroom teacher. He tests positive for the virus. He must now inform his students, his girlfriend and his 3 friends he has been in contact with for the last 14 days – they are known as circle 1. Now the students must inform their parents, their siblings and their friends who they have been in contact with for the last 14 days – they are circle 2 and should also isolate. The girlfriend and friends of Jens must also contact their contacts – who are also in circle 2.
This seems like a very agressive strategy, but the virus we are fighting is very agressive as well.
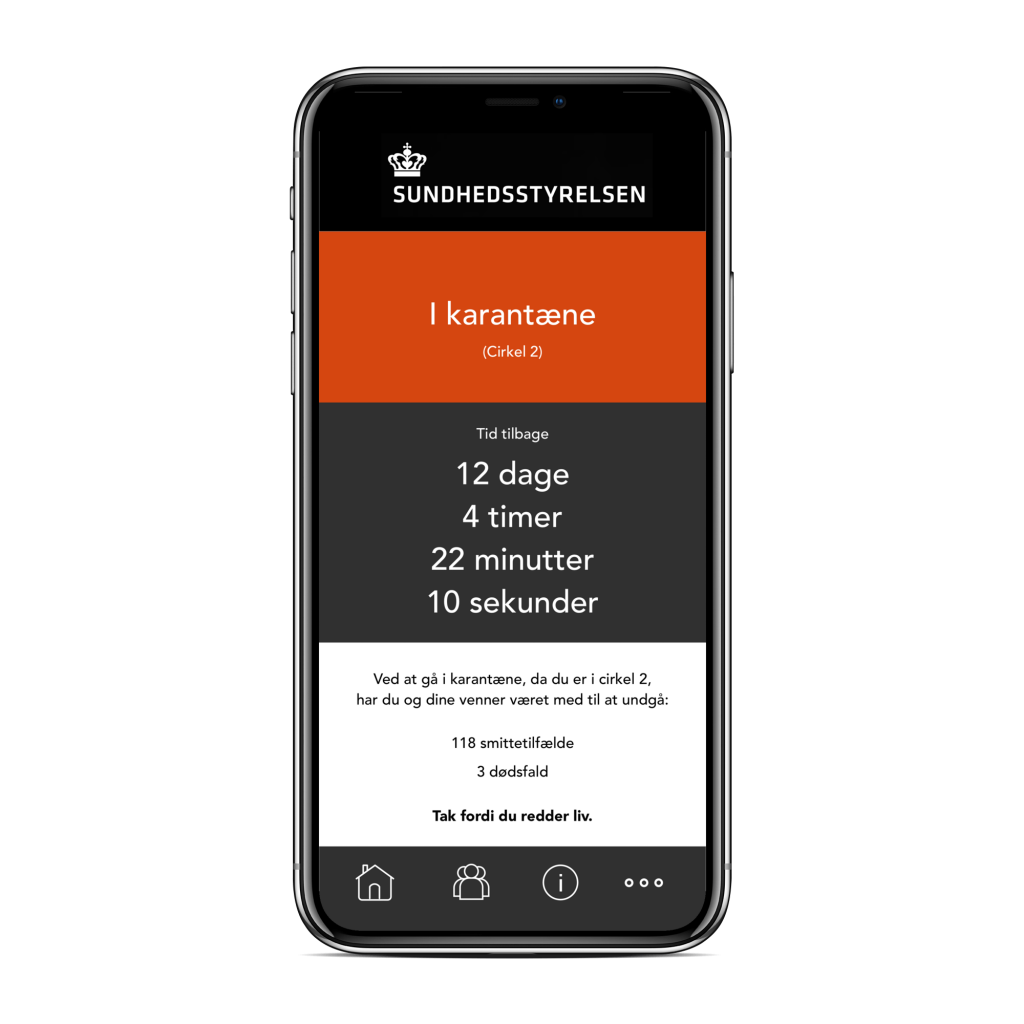
To aid in the process, instead of Jens having to inform every student and contact manually, an app could be developed, where Jens can input the phone number and contact details of his contacts, and they can do the same for their contacts. At the same time, the app could display relevant information and remaining quarantine time (and send a text message to those who have not yet registered with the app, but are in a circle).

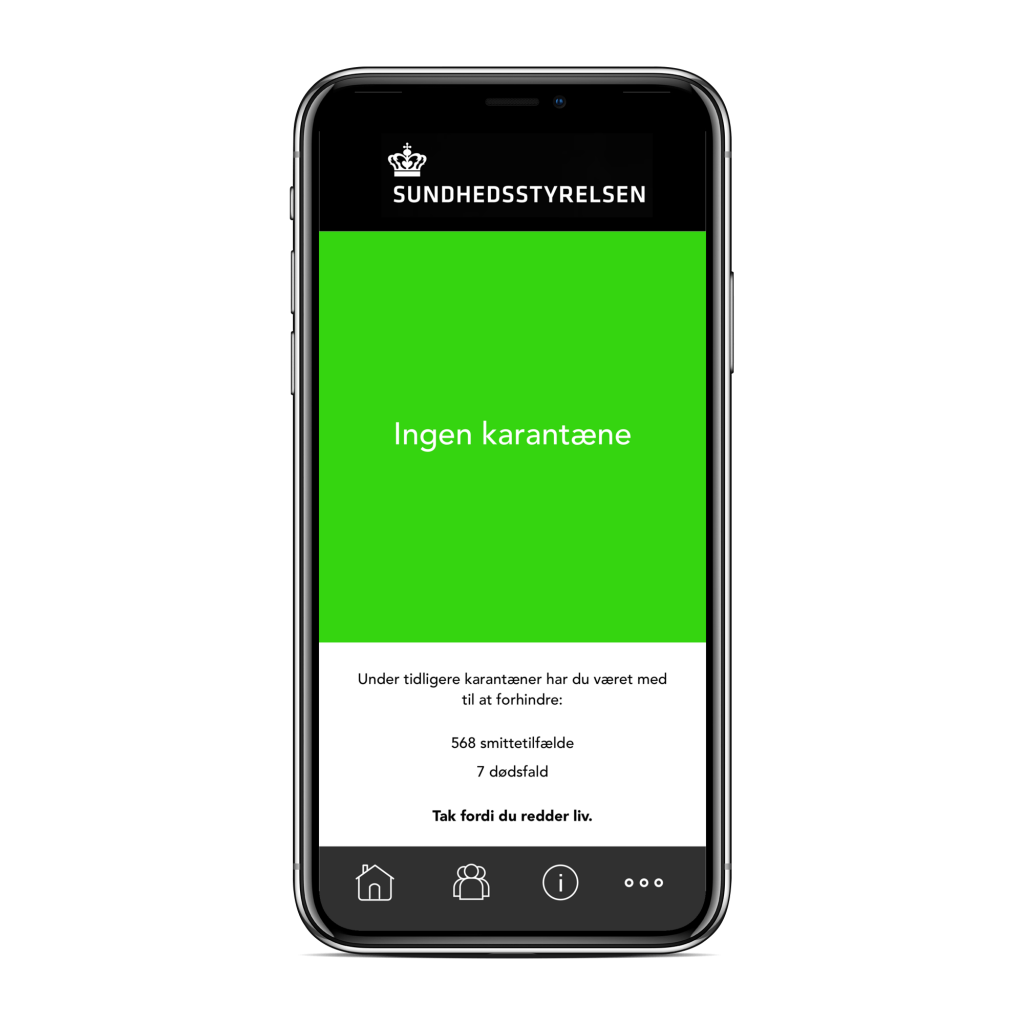
The development of such app should take no more than two weeks and cost no more than 1 million euro (7,5 million DKK).
I realize not everyone will read part 2, and therefore if the reader chooses not to do so, here is the primary objection I imagine the reader has:
“If a person has 10 contacts, and each of those contacts has another 10, this strategy will isolate 100 people for just a single case of the disease. This seems out of proportions and will not work in practice!”.
We need to stand together and fight this disease. We have seen that the whole country can isolate. A hundred people is nowhere close to a whole country. Furthermore, it is up to every person if they want to meet a lot of other people – the more social you are, the higher your risk of quarantine (and the disease), so you are free to just limit your number of contacts, and thereby your own risk of quarantine will drastically decrease.
The strategy does assume some spread of the virus, that are not due to known contacts, and therefore will still be effective with some margin as described in part 2.
Part 2
Until a vaccine or a treatment is reached (and that can be many years), there are only two possible outcomes:
– The virus is contained and eradicated (at least locally eradicated).
– Herd immunity is reached
From Bergamo in Italy, we can see from the numbers that in a worst case scenario, at least approximately 0,5% of those who get the virus dies from it.
The death count in Denmark will therefore be approximately 30.000 people, if we don’t eradicate the virus, and opt for herd immunity. Therefore, we should not opt for herd immunity, as we should not decide to kill 30.000 people.
However, we also need to reopen the economy. Therefore, we need a strategy to contain the virus, and this strategy must be more aggressive than the virus itself.
The virus is very aggressive and has a very large “shadow number” of infected people that does not exhibit any symptoms. That is why, as described in part 1, we must employ a strategy that seems excessive and out of proportion, however for every 1 confirmed case, there are at least 9 around in the circles! Therefore, the double circle isolation.
Mathematically this makes sense. The virus follows an exponential curve (or rather is a logistic function, due to herd immunity). For the sake of simplicity and carefulness, I shall consider the virus to follow an exponential curve, which is safe to assume when the number of infections (and therefore deaths) is small (places like Bergamo and New York cannot assume this and must use logistic functions).
All exponential functions can be described using Eulers constant e:
![]()
Where k is the initial number of new infections, e is Eulers constant, r is the rate with which the virus spreads each day, and t is the number of days since the starting point.
When society is fully open it is apparent that the rate r exceeds 0, and since it is a positive rate, every day the virus spreads more and more. It looks like this:
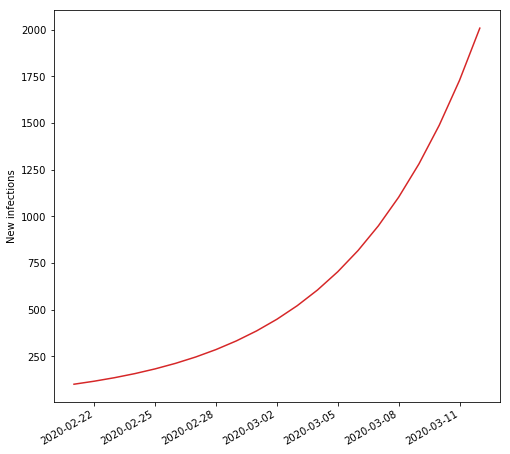
When society goes into lockdown, people still infect each other (lockdown is not perfect), but since the rate r is less than 0, the number of new infections go down. It looks like this:
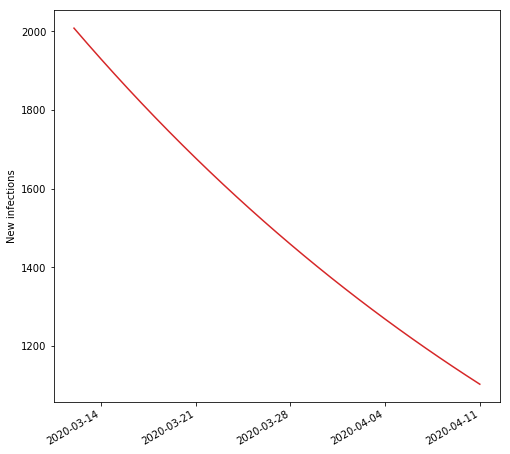
However, upon governments reopening, we are potentially back to an exponential curve. Fully open, lockdown, and reopening combined could look like this:
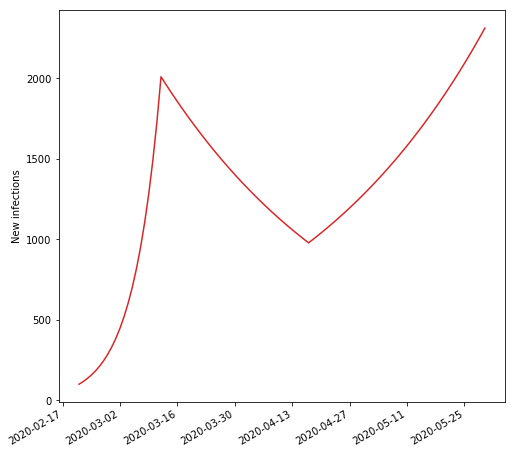
As you see, we might be on the wrong path. We need to reopen, but we also need to contain the virus.
Isolating individual cases does not matter in this case. If we go back to the function we examined before, of new infections:
![]()
We must now realize, that even though this models perfectly the underlying disease spread, only 2 out of 10 persons who are infected show symptoms, and only 1 out of 10 tests positive for the virus. So we have 8 unknowing persons spreading the disease, even if person 1 is tested positive and person 2 self isolates.
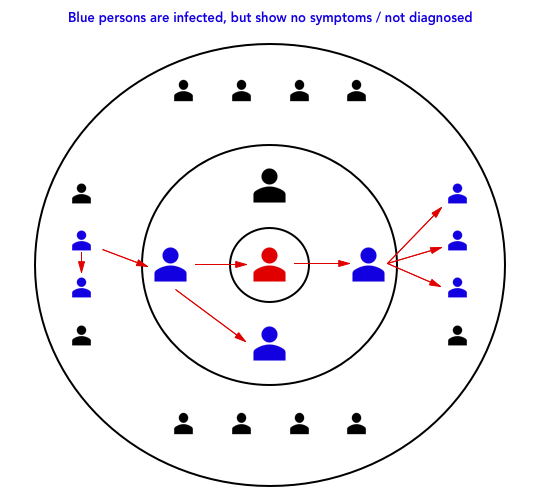
We realize, that we need to isolate more people than just the diagnosed. It is fair to assume that in the majority of cases, the infection stems from someone the diagnosed person has been in contact with. It is also fair to assume, that an infected person has passed the infection on to some contacts:

We now see visualized what we are trying to accomplish. Knowing that many carriers are asymptomatic and undiagnosed, a positive case will be a clue that many around the person are infected but not showing symptoms.
We also see that not only is isolation meant to capture those, who have been infected by the diagnosed person, but also to “go back in time”, and isolate those that were before, and may still have the virus, but are not aware.
There are a lot of variables in this. In the illustration, the diagnosed person has been in contact with 4 people, who in turn each also has been in contact with 4 people, for a total of 16 people plus the diagnosed. Of course, in the real world, someone may have 3 contacts while another person may have 20 direct contacts (as will be the case of a school classroom teacher). Therefore the circles are dynamic.
The dynamic nature of circles is very important. A very social person has the ability to affect many people, and therefore it is only appropriate that the isolation circle grows.
These circles also make sense in another way. It is obvious that the virus does not randomly spread from one person to another 100 kilometers away (sometimes it does happen when one person travels, but most people stay in their hometown). Geography is important, and local infection clusters are much more likely. It is not just random people we are isolating, the additional people we are isolating has a much higher probability of being infected, than if you simply take a random person out of the population and isolate.
Let us consider this figure, where you notice a new blue person (infected with no symptoms) in the right upper corner:
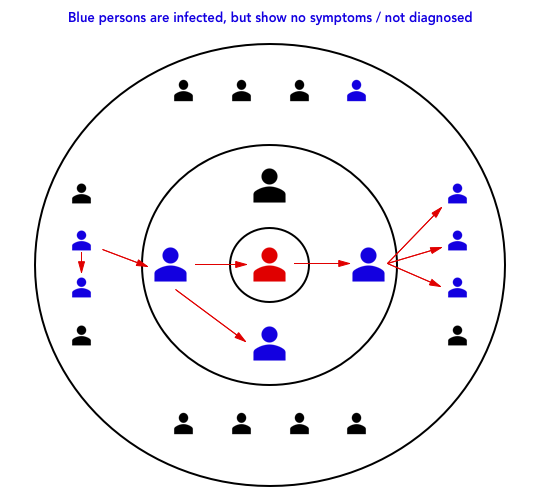
The person in the upper right hand corner is not part of the primary chain of virus spread, but since disease is spreading in the local community, this person have contracted it. However since he is in circle 2 of an infected person, he still needs to isolate and therefore the disease is contained (randomly hitting its target, but not so if you consider that the local community is likely to have more infections).
More time, brainpower and effort is needed to fully describe the mathematics and probabilities behind this idea.
Due to the very time sensitive nature of this event, and a belief that we need to act urgently, I shall just describe the raw mathematics, and quickly demonstrate the consequences. Following the idea of Occam’s razor, it is very brief and simple. The whole idea of isolating two circles should not be discarded, even though the following mathematics may not be completely adequate, and I encourage everyone to improve upon it.
Let

In our equation
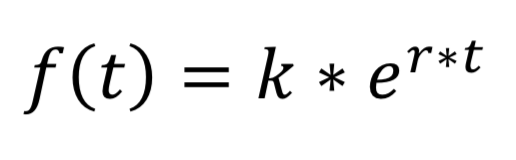
We can now describe r as:
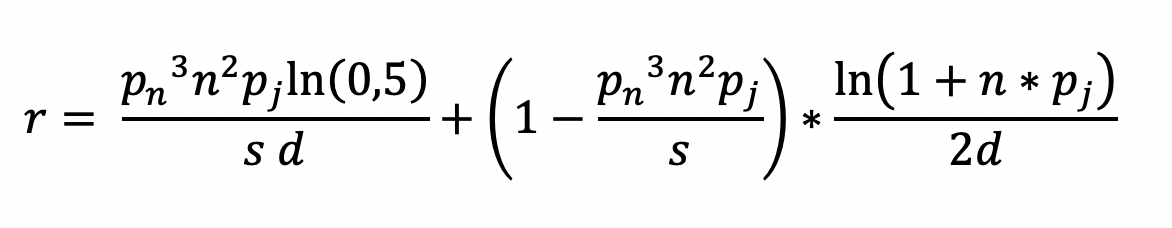
Giving us the final equation:
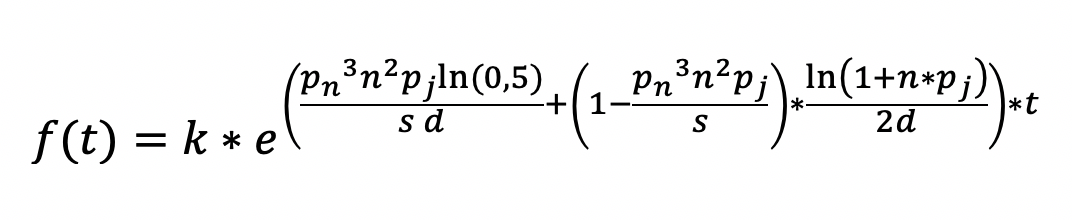
Before we plot this for a range of values, let us just consider what the equation would look like, if only circle 1 is quarantined:
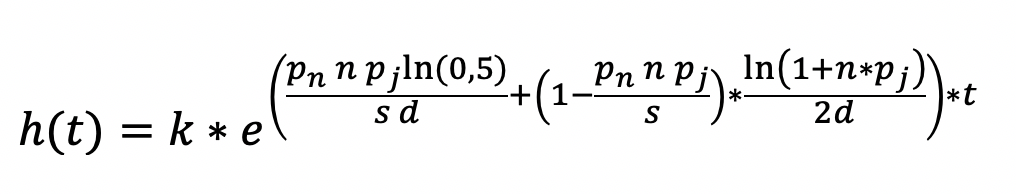
And if we do no isolation at all:
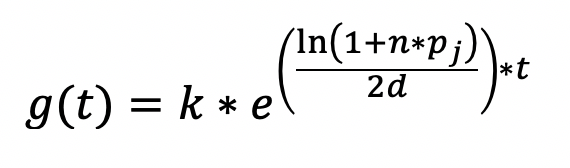
This is in no way a perfect model, and much more work is needed to perfect it. However it does emphasize the power that isolating two circles has.
If we assume some values for our model parameters such as:
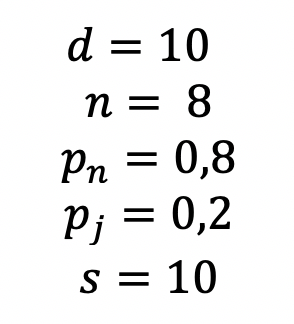
We can plot the expected development:
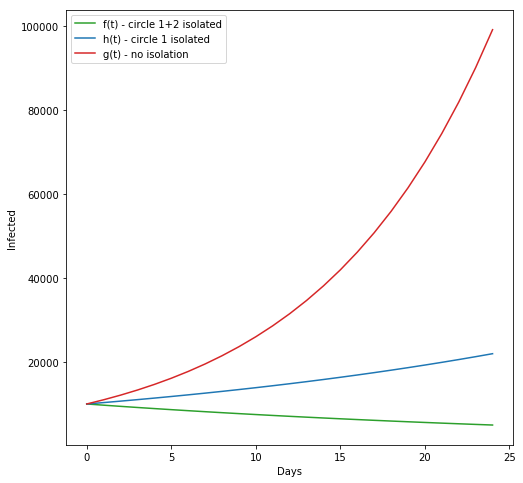
We see that double circle isolation is effective under the assumed circumstances. More work and care is needed to describe the effect of double circle isolation. Any comments or feedback is appreciated.